Esta interpolación se llama interpolación segmentaria o
interpolación por splines. La idea
central es que, en
vez de usar
un solo polinomio
para interpolar los
datos, podemos usar segmentos de polinomios y unirlos adecuadamente para
formar nuestra interpolación. Cabe
mencionar que, entre todas, las
splines cúbicas han
resultado ser las para
aplicaciones como la mencionada anteriormente. Así pues, podemos decir de
manera informal, que una función spline está formada por varios polinomios,
cada uno definido en un intervalo y que se unen entre si bajo ciertas
condiciones de continuidad
Interpolación Segmentaria Lineal
Este es el caso más sencillo. En él, vamos a interpolar una
función f(x) de la que se nos dan un número N de pares (x, f(x)) por los que
tendrá que pasar nuestra función polinómica P(x). Esta serie de funciones
nuestras van a ser lineales, esto es, con grado 1: de la forma P(x) = ax + b.
Definiremos una de estas funciones por cada par de puntos
adyacentes, hasta un total de (N-1)
funciones, haciéndolas pasar obligatoriamente por los puntos que van a
determinarlas, es decir, la función P(x) será el conjunto de segmentos que unen
nodos consecutivos; es por ello que nuestra función será continua en dichos
puntos, pero no derivable en genera.
En este caso, los polinomios P(x) a través de los que
construimos el Spline tienen grado 2. Esto quiere decir, que va a tener la
forma P(x) = ax² + bx + c Como en la interpolación segmentaria lineal, vamos a
tener N-1 ecuaciones (donde N son los puntos sobre los que se define la función).
La interpolación cuadrática nos va a asegurar que la función que nosotros
generemos a trozos con los distintos P(x) va ser continua, ya que para sacar
las condiciones que ajusten el polinomio
idea central es que en vez de usar un solo polinomio para interpolar los datos,
podemos usar segmentos de polinomios y unirlos adecuadamente para formar nuestra
interpolación.
Cabe mencionar que entre todas, las splines cúbicas han resultado ser las más
adecuadas para aplicaciones como la mencionada anteriormente.
Así pues, podemos decir de manera informal, que una funcion spline está formada por
varios polinomios, cada uno definido en un intervalo y que se unen entre si bajo ciertas
condiciones de continuidad.



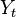
 : variables explicativas, independientes o regresores.
: variables explicativas, independientes o regresores.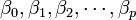 : parámetros, miden la influencia que las variables explicativas tienen sobre el regrediendo.
: parámetros, miden la influencia que las variables explicativas tienen sobre el regrediendo. es la intersección o término "constante", las
es la intersección o término "constante", las  son los parámetros respectivos a cada variable independiente, y
son los parámetros respectivos a cada variable independiente, y  es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.
es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.













.gif)